Thermodynamics and the comparison of hydrocarbon fuels

“What [the National Weather Service] has found, year after year, is that the levels of carbon pollution in our atmosphere have increased dramatically. That science, accumulated and reviewed over decades, tells us that our planet is changing in ways that will have profound impacts on all of humankind.”
Speech delivered by President Obama at Georgetown University, Washington D.C. on Tuesday 25th June 2013.

In the week (week 26, 2013 – Ed) that President Obama announced his bold plan for the US to reduce atmospheric carbon pollution and put the brakes on global warming, what better than a blog post that examines the thermochemical relationship between heat production and CO₂ emissions in hydrocarbon fuels.

But before we begin…

The camping gas cartridge pictured above contains a mixture of butane (C₄H₁₀) and propane (C₃H₈). Combustion of this mixture generates heat, along with the combustion products carbon dioxide and water.

Now here’s a question for you. If instead of the mixture, the cartridge contained only butane, would you expect combustion to produce more or less heat in relation to the amount of carbon dioxide generated?

Base your reasoning solely on the information given above. Jot down your answer, and we will come back to it later.

– – – –

Thermochemistry is the branch of thermodynamics which studies thermal processes associated with chemical reactions and other forms of chemical change. From its beginnings in the 18th century, thermochemistry played an important role in overcoming the misunderstandings about heat which arose from its confusion with the concept of temperature.

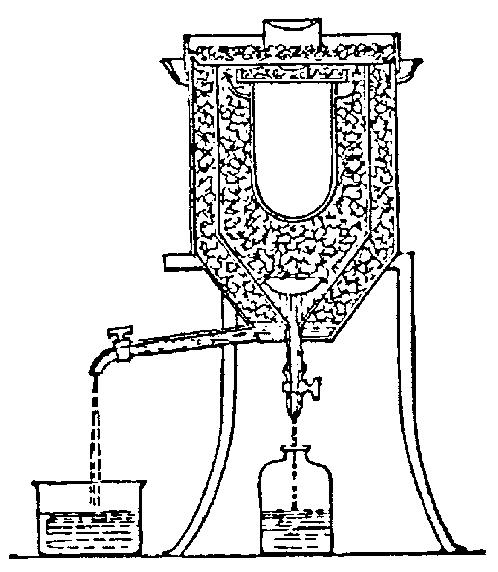
Laplace and Lavoisier’s ice calorimeter of 1780. James Clerk Maxwell wrote of it: “Nothing can be more perfect than the theory and design of this apparatus. It is worthy of Laplace and Lavoisier, and in their hands it furnished good results.”

Through the development and use of the calorimeter, two important early discoveries were made. In France in 1780, those men of genius – Antoine Lavoisier and Pierre-Simon Laplace – discovered that the heat gained or lost in a chemical reaction is equal in magnitude and opposite in sign for the reverse reaction. And in Russia in 1840, the Swiss-born Germain Hess discovered that if a given set of reactants is transformed into a given set of products by more than one reaction path, the total amount of heat gained or lost is the same for each path.

The second of these two discoveries, now called Hess’s law, has for decades been peculiarly subject to factual distortion in science education. Hess measured heat changes at constant pressure (q_p), but because of the later-discovered identity q_p = ΔH, Hess’s law is commonly stated in terms of enthalpy change. Students are thus misled into thinking that Hess discovered an enthalpy summation relation, when in fact he had been dead for 25 years before the concept of enthalpy was first defined by Gibbs in 1875. This kind of timeline falsification, although motivated by an understandable desire to keep things simple in textbooks and internet resources, does the proper study of thermodynamics a disservice in my view.

– – – –

The development in the first half of the 20th century of the concept of the covalent bond led directly to a new class of thermochemical data called bond enthalpies. Tables of these averaged quantities allow the estimation of enthalpy of reaction using the rule:

ΔH_rxn = ΣΔH_{(bonds broken)} – ΣΔH_{(bonds formed)}

Care needs to be taken with average values, since there can be considerable variations in certain circumstances and you need eyes in the back of your head for things like phase transitions and unusual oxidation states, but for applications involving uncomplicated single-phase reactions, bond enthalpies can be a very useful resource.

Here’s an example using an analytical technique of my own. Consider the combustion of alkanes in the vapor phase, which can be represented by the general equation:

C_nH_2n+2(g) + ½(3n+1)O₂(g) → nCO₂(g) + (n+1)H₂O(g)

Say you are interested in the relationship between the heat generated by the reaction (ΔH_rxn) and the number of moles (n) of carbon dioxide produced.

The procedure is as follows. First, expressions in n are found for bonds broken and formed:

bonds broken	total	avg. bond enthalpy
C–H	2n+2	a
O=O	½(3n+1)	b
C–C	n-1	c
bonds formed
C=O	2n	d
O–H	2n+2	e

The enthalpy of reaction ΔH_rxn can then be expressed as the sum of the bond enthalpies of the reactants, minus the sum of the bond enthalpies of the products, all bond enthalpies being regarded as positive quantities.

ΔH_rxn =  [(2n+2)a + ½(3n+1)b + (n-1)c] – [(2n)d + (2n+2)e]    …(1)

The incremental value of ΔH_rxn for an integer increase in n can be found by differentiation:

d(ΔH_rxn)/dn = [2a + (3/2)b + c] – [2d + 2e]    …(2)

It is evident from inspection of (1) that (2) represents the limiting value of ΔH_rxn per mole of CO₂ produced as n becomes very large. This fixes the far end of the alkane scale; the other end is found by setting n=1 in (1):

ΔH_rxn(n=1) = [4a + 2b] – [2d + 4e]    …(3)

By inserting the values of the average bond enthalpies into expressions (3) and (2), the range of ΔH_rxn per mole of CO₂ produced by the combustion of alkanes is determined. The absolute values may not be very accurate, but the trend as n increases will have sufficient accuracy to indicate which alkanes generate the most energy per mole of CO₂ produced.

Note: The analytical technique described above is original work by the author of CarnotCycle. If you make use of it for your own purposes, please include a reference to this blog/blogpost. Many thanks.

– – – –

At a time when atmospheric CO₂ levels have passed the 400 ppm mark for the first time since the Pliocene period, it seems an appropriate moment to take a look at the principal hydrocarbon fuels and see which of them generate most energy in relation to carbon dioxide produced.

Energy generated (kJ)

	Reaction enthalpy	per gram fuel	per mole O2	per mole CO2
Natural gas CH4 + 2O2=CO2 + 2H2O	810	51.6	405	810
Ethanol C2H5OH + 3O2 = 2CO2 + 3H2O	1257	27.3	419	628
Petroleum 2(-CH2-) +3O2 = 2CO2 + 2H2O	1220	43.6	407	610
Coal 4(-CH-) + 5O2 = 4CO2 + 2H2O	2046	39.3	409	512
Cellulose (-CHOH-) + O2 = CO2 + H2O	447	14.9	447	447

According to these figures widely quoted on the internet, natural gas gives the best quotient among the fossil fuels, delivering 42% more energy per mole of CO₂ produced than coal, which explains the “cleaner alternative” phrase favored by energy ministers when asked about all the sudden interest in shale gas.

In terms of transport fuels, there is little difference on this analysis between ethanol and petroleum. The value of bioethanol supplementation of gasoline would appear to be linked more to sustainability and supply security than energy/emission quotient, although for fair comparison one should take biomass origin and CO₂ emissions during industrial processing into the overall reckoning.

Cellulose gives the lowest quotient, although again it must be acknowledged that the carbon it contains came from atmospheric CO₂ in the first place. The only observation I would make about the popular “CO₂-neutral” appellation is that while living plants generally take up CO₂ at average atmospheric concentrations, power stations burning biomass pump out CO₂ at vastly higher concentrations. Under continual operation, a steady-state gradient with a high local CO₂ concentration is likely to be established. If there is water nearby (power stations are often placed next to large water masses for cooling purposes), CO₂ will readily dissolve in it. So in overall terms, CO₂-neutral could actually mean accelerated atmosphere-to-ocean transfer, which in view of the resultant ocean acidification may not be entirely neutral in its environmental impact.

– – – –

One last point to cover is the underlying reason for the differences in energy/emission quotient shown in the final column of the above table. The figures in the penultimate column for energy generated per mole of oxygen consumed show remarkably little variation between fuels, which indicates that the explanation of the difference lies in the other element in the CO₂ molecule – carbon.

The covalently bonded carbon atom can vary in its oxidation state depending on the atoms other than carbon to which it is attached. Bonding to hydrogen decreases the oxidation state, while bonding to oxygen increases it. And this affects the amount of energy released from a hydrocarbon fuel on combustion – the lower the average oxidation number of the carbon, the higher the enthalpy of combustion, and vice versa. The table below demonstrates the correlation nicely.

	kJ per mole of CO2	Avg. oxidation number of carbon in fuel
Natural gas CH4 + 2O2 = CO2+2H2O	810	–4
Ethanol C2H5OH + 3O2 = 2CO2 + 3H2O	628	–2
Petroleum 2(-CH2-) +3O2 = 2CO2 + 2H2O	610	–2
Coal 4(-CH-) + 5O2 = 4CO2 + 2H2O	512	–1
Cellulose (-CHOH-) + O2 = CO2 + H2O	447	0

We have reached the end, so let’s go back to that question posed at the beginning –

“Would you expect butane to produce more or less heat in relation to the amount of carbon dioxide generated than a butane-propane mixture?”

The answer is less heat.

The average oxidation number of carbon in butane(H=10,C=4) is –10/4 = –2.5 while that of propane(H=8,C=3) is –8/3 = –2.67. Butane alone has a less negative (i.e. higher) average carbon oxidation number than any butane-propane mixture, and so should produce less heat  per mole of carbon dioxide generated. Enthalpy of combustion determinations show this prediction to be correct.

– – – –