Special in every way : 7-sided dice

Smarter than the average dice, don’t you think? Just an inch long yet weighing a nicely solid 14 grams, these 7-sided polished bronze stainless steel dice from The Trinket Emporium have a pleasant feel in the hand and roll amazingly well. And while rolling them, one can marvel at the engineering that makes a 7-sided die possible.

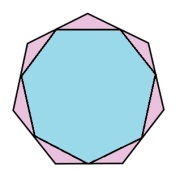
A rolling die with a regular heptagonal cross-section has the geometric property that when it comes to rest on one of its faces, there is no opposite face pointing upwards. This problem is solved by inscribing an inverted heptagonal cross-section area between the end sections on which the die rolls. The result is aesthetically pleasing and practical to play with.

Careful thought has also been given to the order of the numbers, with the even numbers inserted between the odd numbers in reversed order: 1 6 3 4 5 2 7.

Thermodynamic thoughts on Coal Gas

The replacement of wood by coal as the world’s main source of energy stoked the engine of the industrial revolution as the world entered the 19th century. It was known that a flammable gas could be obtained from coal by destructive distillation, and it was not long before enterprising individuals thought of using it for the purposes of illumination. In June 1807, the world’s first demonstration of street lighting by coal gas (town gas in the US) took place at 100 Pall Mall in London. A plaque marks the spot.

This event predated much of the science by which the production and use of energy is understood. The laws of thermodynamics were yet to be formulated, the concept of molecules had yet to be proposed, and physical chemistry as a whole was at a very early stage of its development. The production of coal gas was therefore driven not by scientific knowledge but by utility. Lighting of streets and factories mobilized workforces for longer hours and more productivity, and coal gas provided the means to achieve it. Within a few years of the Pall Mall demonstration, the first public supply of coal gas was established in London at Horseferry Road in Westminster.

Assessing radon risk in your home

Corentium Home Radon Detector

Measuring radon levels in indoor spaces needs a device such as the one illustrated which performs continuous monitoring. This is because levels can and do fluctuate considerably. While the short-term figure goes up and down from day to day, and to a lesser extent from week to week (the display shows alternating 1-day and 7-day figures), the long-term average tends to be quite steady and undulates only gently with the seasons. This is the figure I use to assess radon risk in accordance with official guidelines.

What is radon and where does it come from?

Radon is a chemical element that exists as a colorless odorless radioactive gas. It is not detectable by human senses, but its presence can be measured by radiation monitoring devices designed to detect it. Radon is formed wherever uranium-containing mineral deposits are found. Uranium-238 atoms undergo progressive radioactive decay to atoms of a lower mass number, eventually becoming radium-226. Up to that point, all the decay products are solids and simply coexist with uranium in the mineral. But radium-226 decays to radon-222, which is a gas. Like all gases, it diffuses into spaces available to it and so can leave the uranium deposit and come up from below and into your home.

Sodium bicarbonate and the race to meet climate targets

Acknowledgement: Encyclopedia Britannica

In January 2020, this blog ran a post about Direct Air Capture (DAC), a somewhat misleading term that came into use for processes designed to extract carbon dioxide directly from the atmosphere. Three years later, DAC is one of an array of technologies under the general banner of Carbon Dioxide Removal (CDR), which I gather has not yet been officially adopted by the UNFCCC despite IPCC estimates that CDR will be needed on a big scale to have a hope of reaching Paris Agreement targets.

So what has sodium bicarbonate to do with this? Well, the answer hinges on a point made in the 2020 post that atmospheric CO2 co-exists in dynamic equilibrium with oceanic CO2. Removing CO2 directly from the atmosphere will result in oceanic CO2 outgassing to restore equilibrium. In other words, DAC is insufficient in itself to achieve the desired drawdown. Ocean CDR needs to be brought into the equation.

The official guide to understanding Gibbs

Ever since the works of J. Willard Gibbs were first published, people have struggled to understand him. Back in 1892 Lord Rayleigh, by all accounts a capable physicist and mathematician, complained to Gibbs that his masterwork On the Equilibrium of Heterogeneous Substances was “too condensed and too difficult for most, I might say all, readers”.

In 1927 faculty members at Yale University where Gibbs taught decided to do something about it. A committee was appointed to oversee the creation of a work that would elucidate and facilitate understanding of Gibbs’ writings and the result of their labors was a two-volume Commentary published in 1936. The first volume was on Thermodynamics and the second on Theoretical Physics.

Volume 1 Thermodynamics is over 700 pages long and was written by ten authors of high standing including Edward Guggenheim whose influential textbook Modern Thermodynamics by the Methods of Willard Gibbs had been published by Methuen & Co., London in 1933.