The Phase Rule formula was first stated by the American mathematical physicist Josiah Willard Gibbs in his monumental masterwork On the Equilibrium of Heterogeneous Substances (1875-1878), in which he almost single-handedly laid the theoretical foundations of chemical thermodynamics.
In a paragraph under the heading “On Coexistent Phases of Matter”, Gibbs gives the derivation of his famous formula in just 77 words. Of all the many Phase Rule proofs in the thermodynamic literature, it is one of the simplest and shortest. And yet textbooks of physical science have consistently overlooked it in favor of more complicated, less lucid derivations.
To redress this long-standing discourtesy to Gibbs, CarnotCycle here presents Gibbs’ original derivation of the Phase Rule in an up-to-date form. His purely prose description has been supplemented with clarifying mathematical content, and the outmoded symbols used in the single equation to which he refers have been replaced with their modern equivalents.
– – – –
Gibbs’ derivation
Gibbs begins by introducing the term phase to refer solely to the thermodynamic state and composition of a body (solid, liquid or vapor) without regard to its quantity. So defined, a phase cannot be described in terms of extensive variables like volume and mass, since these vary with quantity. A phase can only be described in terms of intensive variables like temperature and pressure, which do not vary with quantity.
To derive the Phase Rule, Gibbs chooses as his starting point equation 97 from his treatise, now known as the Gibbs-Duhem equation
This general thermodynamic equation, which relates to a single phase, connects the intensive variables temperature T, pressure P, and chemical potential μ where μn is the potential of the nth component substance. Any possible variations of these quantities sum to zero, indicating a phase in internal equilibrium.
If there are n independent component substances, the phase has a total of n+2 variables
These quantities are not all independently variable however, because they are related by the Gibbs-Duhem equation. If all but one of the quantities are varied, the variation of the last is given by the equation. A single-phase system is thus capable of (n+2) – 1 independent variations.
Now suppose we have two phases, each containing the same n components, in coexistent equilibrium with each other. Signifying one phase by a single prime and the other by a double prime we may write
since this is the definition of equilibrium between phases. So in the two-phase system the total number of variables remains unchanged at n+2, but there are now two Gibbs-Duhem equations, one for each phase. It follows that if all but two of the quantities are varied, the variations of the last two are given by the two equations. A two-phase system is thus capable of (n+2) – 2 independent variations.
It is evident from the foregoing that regardless of the number of coexistent phases in equilibrium, the total number of variables will still be n+2 while the number subtracted will be equal to the number of Gibbs-Duhem equations i.e. one for each phase.
A system of r coexistent phases is thus capable of n+2 – r independent variations, which are also called degrees of freedom (F). Therefore
This is the Phase Rule as derived by Gibbs himself. In contemporary textbooks it is usually written
where C is the number of independent components and P is the number of phases in coexistent equilibrium.
– – – –
Update

– – – –
P Mander February 2015


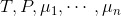



Very insightful! Just discovered this blog today with this article! Must thank you for these gems!
LikeLike
Reblogged this on nebusresearch and commented:
I knew I’d been forgetting something about the end of summer. I’m embarrassed again it was Peter Mander’s Carnot Cycle blog resuming its discussions of thermodynamics.
The September article is about Gibbs’s phase rule. Gibbs here is Josiah Willard Gibbs, who established much of the mathematical vocabulary of thermodynamics. The phase rule here talks about the change of a substance from one phase to another. The classic example is water changing from liquid to solid, or solid to gas, or gas to liquid. Everything does that for some combinations of pressure and temperature and available volume. It’s just a good example because we can see those phase transitions happen whenever we want.
The question that feels natural to mathematicians, and physicists, is about degrees of freedom. Suppose that we’re able take a substance and change its temperature or its volume or its pressure. How many of those things can we change at once without making the material different? And the phase rule is a way to calculate that. It’s not always the same number because at some combinations of pressure and temperature and volume the substance can be equally well either liquid or gas, or be gas or solid, or be solid or liquid. These represent phase transitions, melting or solidifying or evaporating. There’s even one combination — the triple point — where the material can be solid, liquid, or gas simultaneously.
Carnot Cycle presents the way that Gibbs originally derived his phase rule. And it’s remarkably neat and clean and accessible. The meat of it is really a matter of counting, keeping track of how much information we have and how much we want and looking at the difference between the things. I recommend reading it even if you are somehow not familiar with differential forms. Simply trust that a “d” followed by some other letter (or a letter with a subscript) is some quantity whose value we might be interested in, and you should follow the reasoning well.
LikeLike
Strangely I can follow Gibbs’ derivation. Usually I get lost when trying to follow the work of the old school originators of thermo, pchem, etc.
LikeLike